The temporal coherence can be seen as a
phase decorrelation of each frequency light component. As an example, a light
source with only five monochromatic components of the same intensity and
different wavelength li is considered.
Fig. 4-4 Interference amplitude for five different frequencies (thin gray
lines) and amplitude sum (thick black line); the normalized distance
corresponds to twice the distance divided by the average wavelength
Fig. 4-4 shows the interference
signals for each monochromatic component (thin grey lines) and the normalized
total intensity (thick black line). The normalized distance is defined as
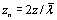where
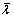is the central wavelength. The interference
signal for the monochromatic components is a cosinus with a period proportional
to the wavelength. A perfect phase matching between the components is observed
at zn = 0 but for an increasing distance |zn|,
the phase matching degrades and the partially destructive addition explains the
modulation amplitude drop of the total intensity.
|
